2月14日,情人节。
在一个以“亲吻”命名的问题上,人工智能与数学完成了一次“深度拥抱”。
1694年,牛顿和格雷戈里在剑桥提出一个问题:在一颗中心球周围,最多能紧贴放置多少颗相同的球?这就是三维空间的“亲吻数问题”(Kissing Number Problem, KNP)。
牛顿认为答案是12,格雷戈里则认为可能是13,直到1953年,数学家才彻底证实了牛顿的猜测。传奇数学家保罗·埃尔德什曾言,离散几何或许就始于这场著名的“12对13”之争。
当维度升高,问题迅速进入“无人区”。过去50年,亲吻数构造仅有7次实质性进展,而且每次依赖完全不同的方法,作用于临近维度,难以迁移与复用。
如今,上海科学智能研究院(下称上智院)与北京大学、复旦大学的联合研究团队设计了PackingStar强化学习系统,在12、13、14、17、20、21、25–31维等多个维度刷新亲吻数与广义亲吻数纪录,实现数学结构领域罕见的多维系统性突破。
这是一次纪录更新,亦是方法论的跃迁、AI for Math范式的一次前移。

两个智能体在高维空间的
如果要给PackingStar找一个情人节比喻,那大概是:它不是单一模型完成的突破,而是两个智能体的共舞协作。
研究团队将高维几何问题转化为余弦矩阵填充问题,并设计了一套多智能体强化学习架构:
Player 1(填充智能体):像在棋盘上落子一样,它不断在矩阵中填入数值,相当于在高维空间里摆放球体,快速生成候选结构。
Player 2(修剪智能体):它负责几何分析,识别不合理的填充,删去次优结构,再把问题交还给Player 1重新优化。
不断试探,不断调整。
这和很多CP之间的默契其实很像:一个大胆尝试,一个冷静校准;一个推进结构,一个压缩噪声。
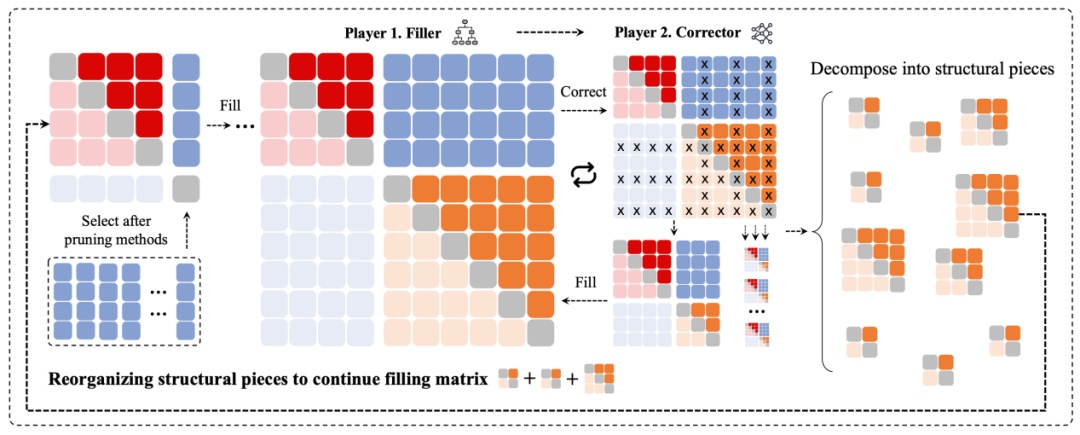
(矩阵填充双人游戏)
在“填充—修剪—解构—再填充”的循环迭代中,高维空间原本几乎不可触达的搜索难度被逐步压缩。复杂几何问题,被转化为一场可以训练、可以优化的多智能体游戏。
关键在于:问题被重新定义——复杂几何,被转化为适合GPU并行计算的代数任务。
这一转化,是PackingStar能够规模化突破的前提,也是方法论的核心创新。
一场AI与Math的
成果层面,PackingStar实现的是多维度、成体系的纪录刷新:
在25–31维连续刷新世界纪录;
打破14维与17维“两球亲吻数”纪录;
打破12维、20维、21维“三球亲吻数”纪录;
在13维发现优于1971年以来所有有理结构的新构型;
在多个维度中发现6000余个新结构。
这些成果获得MIT教授、离散几何领域权威Henry Cohn高度评价,并被收录至其维护的权威榜单。Cohn在PackingStar发现的结构基础之上,自己又打破了两个维度的广义亲吻数纪录。
左右滑动,查看更多
更重要的是,这些突破并非单点发现,而是呈现出系统性特征。
在亲吻数问题的三百年历史中,这样的跨维度连续推进极为罕见。在PackingStar出现之前,32维以下仅6次实质性改进,而且每一次几乎都是孤立突破,依赖完全不同的数学技巧,难以迁移。而PackingStar在多个维度同步推进,揭示出不同维度之间潜藏的结构关联,使构型不再彼此封闭,而形成可迁移、可比较、可演化的几何网络。
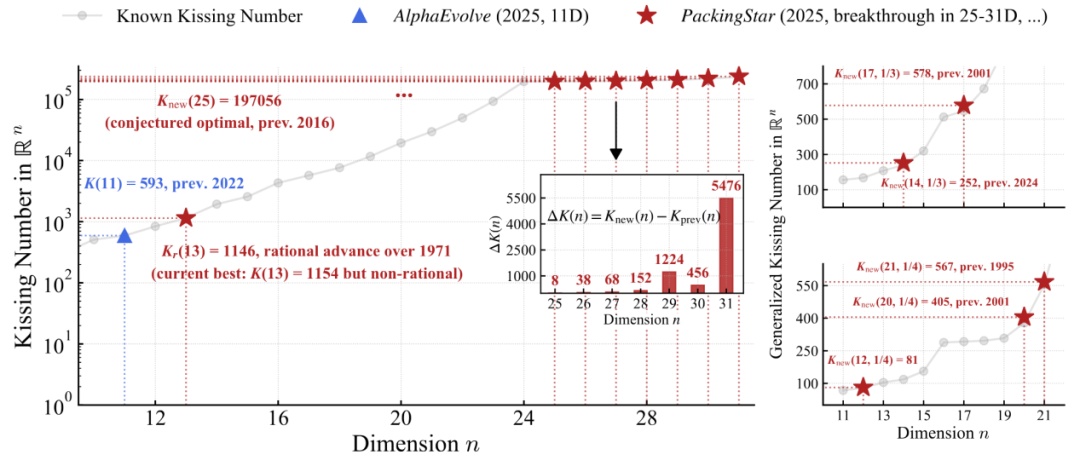
(AI在亲吻数问题上的突破)
近年来,全球AI for Math领域不断取得进展:
AlphaGeometry通过反向合成数据推动欧氏几何求解,AlphaTensor优化矩阵乘法,FunSearch刷新部分组合问题,AlphaEvolve在11维亲吻数实现单点提升。
相对而言,亲吻数问题具有更高难度特征。它是三百年历史的经典难题,进展极度稀缺,几乎无法通过反向合成数据进行训练,传统方法高度依赖全局对称结构。
PackingStar面对的是一个缺乏数据、结构高度复杂的高维组合优化问题。
它不仅刷新了纪录,更首次实现了对非对称规则构型的系统性搜索与生成。AI不再只是优化已有结构,而是在高维空间中主动构造新的几何可能。
如果说此前的代表性工作证明AI可以“解题”,那么PackingStar进一步证明:AI可以参与“构造”,并在缺乏可学习样本的条件下形成可持续的探索路径。
这,是AI for Math范式的一次前移。
一场人类与机器的
菲尔兹奖得主William Thurston说过:“数学并不是关于数字、方程、计算或算法的;它关乎的是理解。”
在PackingStar的实践中,研究团队对这句话有了更深体会。
科学智能的创新突破,并不是等待AI“突然显灵”,而是一个人机闭环:
构造(AI):在巨大空间中学习高速生成结构;
洞察(人类):理解AI结果,提出数学直觉,提炼理论逻辑。
团队核心成员、上智院AI科学家陶兆巍出身数学专业,在研究过程中常常与AI“较劲”。如果自己在某一步的判断优于AI,就尝试把这种直觉转化为算法,再注入系统。PackingStar中的Player 2,正是在这样的反复互动中诞生。
这不是替代关系,而是互相塑造。
例如,在12维81球构型问题上,PackingStar首先发现对称性极弱的新纪录结构。虽看似杂乱,但在进一步分析后,团队发现了其隐藏规律,并引入经典Schläfli构型重新搜索,最终找到高度对称的新结构,并推广至20维与21维的新纪录构型。
而项目组长、上智院AI Math青年研究员、北京大学博士生马成栋则更多感受到另一种震撼。当AI不断突破人类直觉的边界时,甚至连解释都变得困难:“比如某些结构中没有一个球有对径球,但却保持了极高的对称性。它不只是超越了人类可以构造的范围,有时候你甚至很难第一时间解释它为什么成立。”
这种体验,对研究团队来说既是挑战,也是推动力。
人类科学家的角色,也在变化——
从独自推演与构造,转向与AI在数学的宇宙里协同理解、深度共进。
“鹊桥工程”
情人节的故事里,总有一座鹊桥。
在PackingStar背后,也有一座“工程之桥”。
当维度提升至18、19维时,搜索空间急剧膨胀,计算瓶颈成为现实挑战。工程团队对底层算子进行了系统优化,提升计算效率、保障大规模运行:
重写关键CUDA Kernel;
消除显存冗余读写;
提升GPU利用率;
构建自动Checkpoint机制,保障千卡规模长周期运行稳定。
由此,项目的搜索效率提升2–3倍,累计节省超过10万GPU卡时。计算效率和内存优化让团队在未解问题的每一个阶段都能看得更远,从而更快地扫清障碍、识别出关键的数学结构。
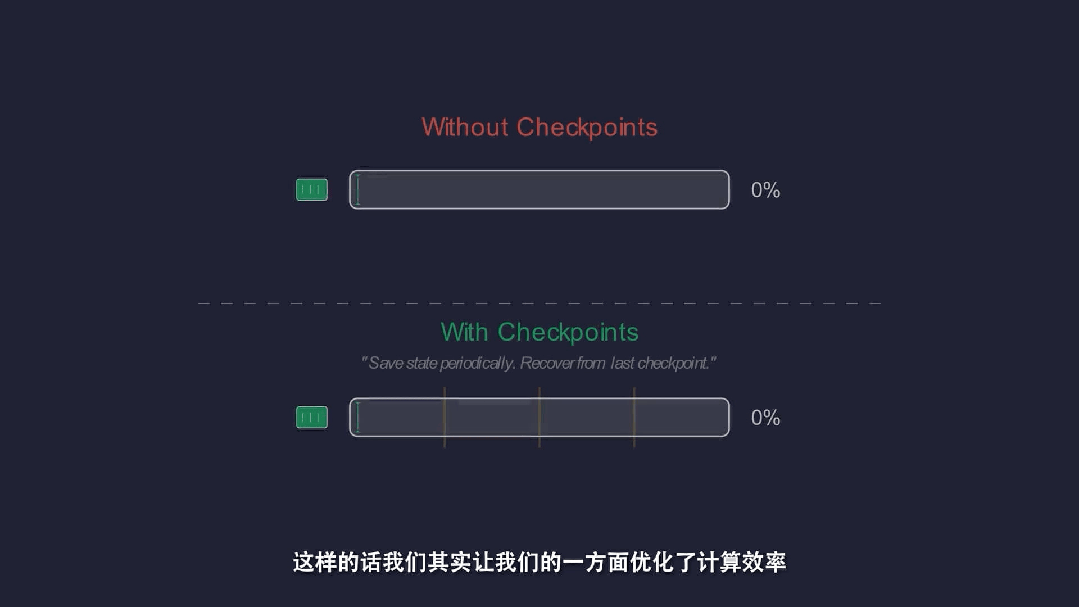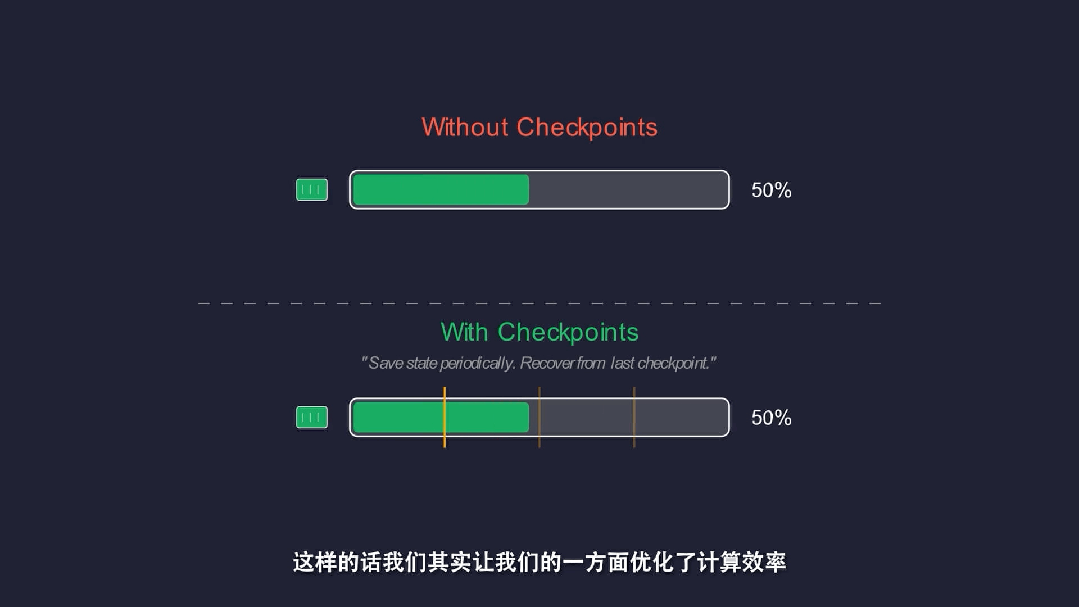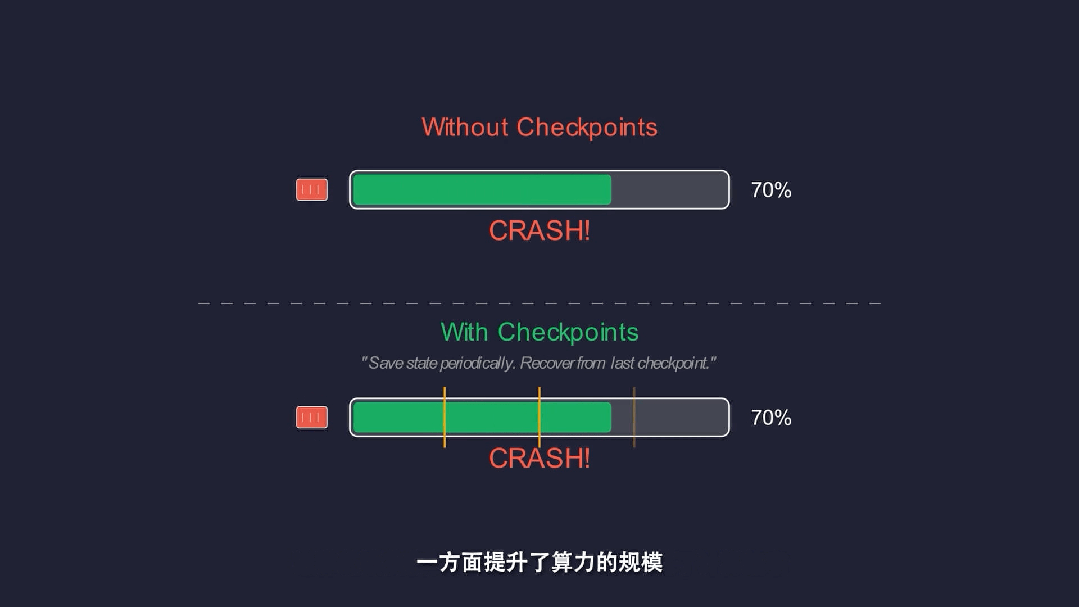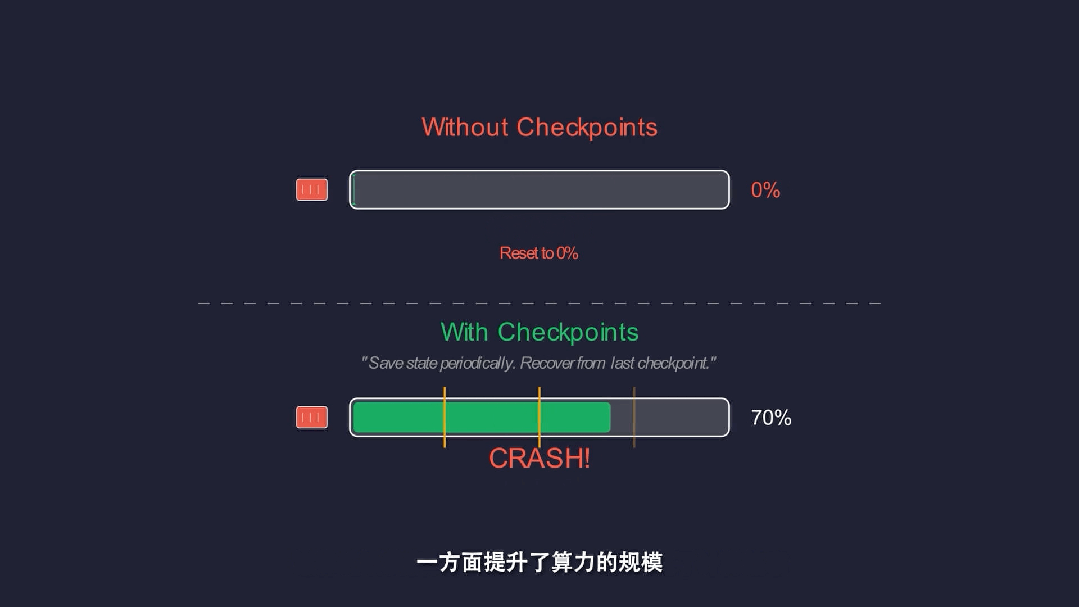
工程优化不是配角,而是科学突破的基础设施。
科学智算连接了算法与现实算力,带来大规模加速,让数学探索具备可持续性。
在星河启智科学智能开放平台的支撑下,相关算子与方法沉淀为可复用能力,为更多科学问题提供工具基础。
今天是情人节。
我们借“亲吻数”这个名字,讲了一个人工智能与数学的故事。
然而值得关注的,不只有一个节日,还有不同人的彼此照见,不同角色和领域之间的协作与理解:
AI、数学与工程,算法与结构,直觉与计算,青年科学家与机器系统,理论与实践……“我”和“你”。
当边界被打破,知识开始互相拥抱。
PackingStar的意义,不止于刷新纪录,还在于证明:AI-领域-工程可以形成稳定协作的共进机制。
在这个有情的世界里,愿每一次跨界相遇,都能成为一次深度理解;也愿每一次严肃的科学探索,都带着一点点温柔。
为了回答牛顿三百年前的一个问题,
一群青年让AI学会了创造高维几何结构。
科研纪录短片《Packing Star》,
带你回到1694年,也带你遨游数学宇宙。
(PackingStar团队的科研青年们,从右至左为:陶兆巍、刘明灏、马成栋、李鹏宇、毛子皓、陈浩钧)
欢迎转发,但请注明出处“上海经信委”
觉得不错请点赞!